



“Baví mne věci kolem sebe pozorovat a hledat souvislosti, měřit, počítat a optimalizovat,” říká v novém rozhovoru Ondřej Kubíček, náš Product Owner.

Co je to korelace, k čemu může být užitečná, jaké druhy korelace existují, jak je používat a interpretovat? Odpověď na tyto a některé další otázky nabízí následující text od našeho kolegy Martina Roseckého.
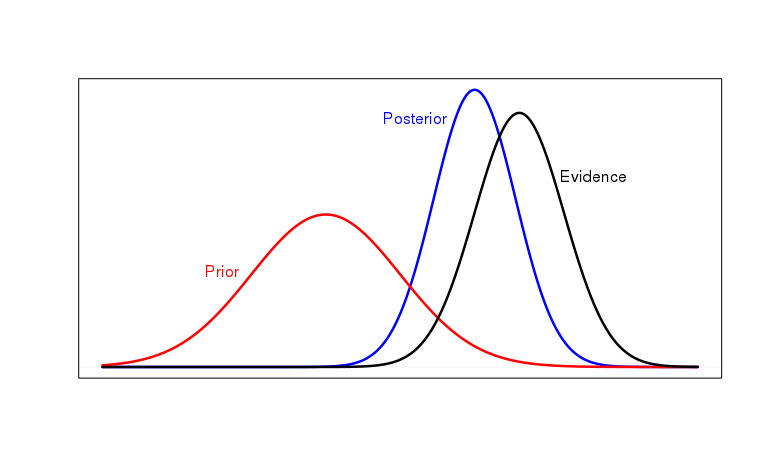
Podívejme se krátce na vývoj vztahu klasického (frekvenčního, Fisherovského) a Bayesovského přístupu ke statistice. V nedávné minulosti se vedly bouřlivé odborné a často až filozoficky orientované debaty, které pak měly za důsledek postupné změny nejen v samotné analýze dat, ale i ve výuce statistiky.



Ondro, co tě baví na práci Product Ownera?
Pracoval jsem na řadě projektů jako byznys analytik, product owner nebo projektový manažer. Baví mně poznávat, vylepšovat i navrhovat nové podnikové procesy. Nejlépe takové, kde je brzy vidět dopad zavedených změn a dá se objektivně změřit. Rychlá zpětná vazba je podle mně podmínkou pro udržení pozornosti a nadšení jak vývojového týmu, tak i zadavatele. Při diskuzích nad zjištěnými výsledky se v lidech probouzí kreativita a padají další a ještě lepší nápady pro další rozvoj.
Baví mne věci kolem sebe pozorovat a hledat souvislosti, měřit, počítat a optimalizovat. Jednoho dne uzrálo rozhodnutí, že budu pracovat na projektech, kde propojím svůj koníček a práci. Energetice jsem se začal věnovat ve společnosti Mycroft Mind, abych následně navázal spolupráci se společností CzechMath.
Máme tým složený z matematiků a vývojářů s bohatými zkušenostmi s modelováním, simulacemi a optimalizací.
Spolu s CzechMath zpracováváme energetické studie na míru konkrétním zákazníkům a jejich energetickému portfoliu. Pomáháme tak vybrat vhodné technologie a správně je dimenzovat s ohledem na zvolený cíl – úsporu, návratnost nebo soběstačnost. Pracujeme s fotovoltaickou výrobou elektřiny, kogenerací, tepelným hospodářstvím a akumulací elektřiny do baterií i tepla. Zohledňujeme přitom mj. i chování zákazníků, zejména průběh výroby a spotřeby energií v čase. Máme za sebou projekty pro municipality, průmyslové areály, bytové i rodinné domy.

Jakému projektu se teď věnujete?
Věnujeme se vývoji systému pro chytré řízení a optimalizaci energetického portfolia – Energy Portfolio Manager, EPM. Systém pracuje mimo jiné s řiditelnou spotřebou, výrobou a akumulací elektrické energie a nákupem a prodejem elektřiny za proměnlivé ceny. Někdy je výhodné energii akumulovat na později, jindy rovnou spotřebovat, přeměnit na teplo nebo prodat do sítě. Část spotřeby elektrické energie lze odložit nebo naopak uspíšit bez dopadu na komfort uživatele budovy – např. ohřev teplé vody lze přesouvat v čase, aniž by to někdo zaznamenal. Vše záleží na řadě podmínek – počasí a očekávané výrobě i spotřebě elektřiny, spotřebě teplé vody během dne aj. Dalším důležitým vstupem je cena elektřiny v čase – doba platnosti vysokého a nízkého tarifu, výkupní cena elektřiny, příp. i průběh spotových cen elektřiny na burze. Jedná se o velice komplexní optimalizační problém.
Někdo chce ušetřit na platbách za energie, jiný chce snížit spotřebu elektřiny ze sítě a tím i snížit svou uhlíkovou stopu. Dalšímu jde o dosažení vyšší energetické bezpečnosti a vyšší míry soběstačnosti. Někdy lze dosáhnout více cílů zároveň, jindy jdou proti sobě. Pro každé kritérium probíhá optimalizace jiným způsobem a tomu odpovídá zvolená strategie řízení. Rostoucí ceny energií přínosy takových opatření ještě navýšily.
EPM hledí do budoucnosti a krom optimalizace energetiky jednotlivých staveb a areálů počítá i s nástupem komunitní energetiky. Díky ní si budete moci vybrat komu a za jakých podmínek postoupíte přebytky své výroby elektřiny. Případně se v rámci své komunity (rodiny, sousedství, městské části atp.) dohodnete na pořízení zdroje elektrické energie, jehož výrobu budete v rámci komunity za domluvených podmínek sdílet. Podmínkou je ovšem vytvoření odpovídajícího legislativního prostředí a rozšíření smart meteringu – chytrých elektroměrů.

Můj názor je, že když už je lidstvo závislé na výrobě a spotřebě elektřiny, ať je jí potřeba vyrobit co nejméně a daří se to co možná nejčistší cestou. Čím se podaří využít obnovitelné zdroje energie efektivněji, tím menší bude potřeba využívat méně čisté zdroje energie. Čím jsou obnovitelné zdroje pro své provozovatele výhodnější, tím více se rozšíří a tím čistší energetický mix získáme.



TLDR:
V životě člověka je poměrně běžné hledat a posuzovat souvislosti mezi rozličnými jevy, ať už si to uvědomujeme, nebo ne. Příkladem mohou být otázky jako: Nakolik souvisí výsledky ve volebním průzkumu či modelu s reálným výsledkem voleb a jak se tato souvislost mění v čase? Jak moc mi bude špatně, když zkonzumuji větší množství jídla či alkoholu než obvykle? Jakým směrem a jak výrazně se pohne cena kryptoměny na základě tweetu Elona Muska? Jak velký přínos bude mít, když se budu večer před písemkou učit místo toho, abych navštívil oblíbené restaurační zařízení? Lze z níže uvedené fotografie usoudit, že kočky způsobují pády střech?
#Correlation is not #Causation pic.twitter.com/3csdhaGmee
— john gonder infosec.exchange/@packetlevel (@packetlevel) October 22, 2021
Výše zmíněné otázky více či méně míří na koncept korelace. Korelace by se v obecném smyslu dala popsat jako měřítko, které dokáže vystihnout toto chování: když hodnota jedné proměnná roste, roste (pozitivní korelace), příp. klesá (negativní korelace) i druhá. Laicky řečeno je korelace hodnota, která říká, jak moc spolu sledované proměnné souvisí.
Příkladem může být třeba množství prodané zmrzliny a teplota vzduchu. Dá se očekávat, že v teplejších dnech bude množství prodané zmrzliny vyšší oproti chladnějším dnům.
Velmi důležitým pojmem při použití korelace je i kauzalita neboli příčinnost. Ta zjednodušeně řečeno říká, zda je jeden jev příčinnou druhého (v uvedeném příkladu vyšší teplota způsobuje vyšší prodej zmrzlin). Narozdíl od korelace však kauzalita není symetrická (z výše uvedeného je zřejmé, že ani symetrická být nemůže). Navíc “přítomnost” korelace neznamená, že nutně mezi oběma proměnnými existuje i kauzální vztah (odtud ono známé – korelace neimplikuje kauzalitu). Co to znamená prakticky? Když k uvedenému příkladu přidáme ještě údaje o počtu požárů, mohlo by někoho na základě korelace napadnout, že v rámci prevence požárů bude dobré zakázat prodej zmrzliny, což zřejmě nebude příliš funkční opatření.
Pojem korelace se v médiích objevuje zejména v souvislosti s děním na trzích, se studiemi týkajícími se vlivu nějakého faktoru na zdraví člověka či se sociologickými/ psychologickými studiemi. Tento pojem standardně bývá i součástí základních kurzů statistiky a pravděpodobnosti, přičemž se v drtivé většině jedná o tzv. Pearsonův korelační koeficient. Jeho praktické využití má však více úskalí než se může na první pohled zdát (zvlášť pro člověka bez hlubších znalostí a zkušeností).
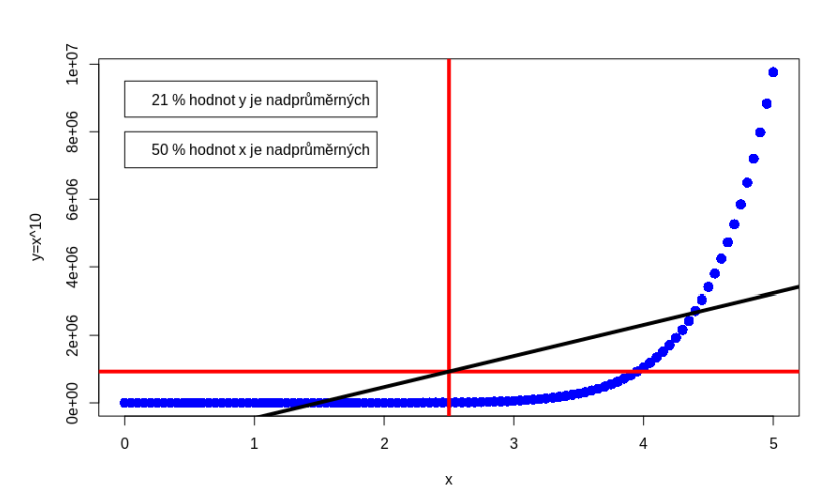
Pearsonův korelační koeficient závisí zejména na hodnotě kovariance. Její hodnota roste v případě, že jsou hodnoty sledovaných proměnných obě vyšší než průměr, resp. nižší než průměr, v opačném případě hodnota kovariance klesá. Toto chování ukazuje na důležitost 2 základních předpokladů: linearita závislosti mezi proměnnými a normalita sdruženého rozdělení zkoumaných proměnných. Hodnoty směrodatné odchylky, příp. rozptylu, zajišťují pouze škálování kovariance na interval [-1,1]. V případě porušení uvedených předpokladů může být chování Pearsonova korelačního koeficientu značně neočekávané (viz obr. 1, pro který vychází hodnota korelačního koeficientu rovna 0,66, přičemž je zde patrná dokonalá exponenciální závislost).
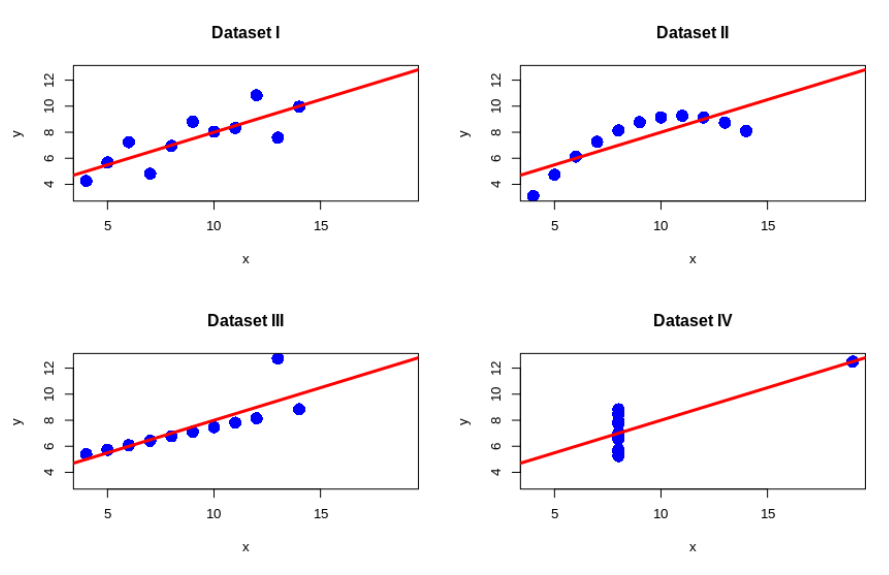
Zmíněné problémy nejsou ničím novým pod sluncem. Poměrně známý je příklad Anscombe (1973, [1]), který uvádí čtveřici statistických souborů (viz obr. 2). Tyto soubory mají stejné nebo alespoň velmi podobné hodnoty základních sumarizačních charakteristik (výběrové průměry, rozptyly, korelaci), a také (lineární) regresní model (včetně koeficientu determinace), viz tab. 1. Tento příklad, podobně jako projekt Datasaurus ([2], viz obr. 3), primárně nekritizuje používání (Pearsonova) korelačního koeficientu. Snaží se spíše upozornit na nutnost vizualizace dat oproti jejich prostému shrnutí prostřednictvím základních měřítek (viz obě zmíněné datové sady).
| Charakteristika | Hodnota | Přesnost |
|---|---|---|
| Průměr x | 9 | přesné |
| Rozptyl x | 11 | přesné |
| Průměr y | 7,5 | 2 desetinná místa |
| Rozptyl y | 4,125 | ± 0,003 |
| Korelace | 0,816 | 3 desetinná místa |
| Lineární regresní model | y = 3,00 + 0,50x | 2 resp. 3 desetinná místa |
| R2 | 0,67 | 2 desetinná místa |

V roce 2019 se Pearsonův korelační koeficient ocitl pod silnou kritikou N. N. Taleba. Přesněji řečeno šlo spíše o kritiku jeho nesprávného používání (při nesplnění předpokladů), zejména v sociálních vědách.
Zde byly prezentovány a demonstrovány mj. následující problémy:
Obecným problémem s korelacemi (zejména při menším množství dat) jsou tzv. spurious correlations. Ty odkazují na situace, kdy jsou sice nějaké proměnné silně korelovány, ale neexistuje mezi nimi žádný kauzální vztah (např. počet absolventů PhD studia a množství uranu uloženého v amerických jaderných elektrárnách). Takové situace mohou vzniknout pouze dílem náhody (při dostatečném množství náhodně generovaných proměnných se dříve nebo později objeví silná korelace). Dalším případem falešných korelací je situace, kdy jsou 2 proměnné (např. počet požárů a množství prodané zmrzliny) „svázány” prostřednictvím třetí proměnné (zde např. průměrná denní teplota), která buď není nebo nemůže být pozorována.
V této části budou stručně popsána další vybraná měřítka pro měření závislosti v datech. Spearmanův korelační koeficient se používá jako nejčastější alternativa k Pearsonovu, zejména pokud dojde k porušení jeho předpokladů. Vzdálenostní korelace je novým a nepříliš známým přístupem k tomuto problému. Vzájemná informace je pak navrhována N. N. Talebem.
Nejprve se vraťme k problému nutnosti vizualizace dat, konkrétně k Anscombově kvartetu (viz obr. 2). Výše byla zmíněna neschopnost Pearsonova korelačního koeficientu rozlišit typově výrazně odlišné závislosti. Nabízí se tedy jednoduchá otázka: dokáže některé ze zkoumaných měřítek odhalit, že se jedná o výrazně odlišné závislosti? Jako vodítko nám poslouží výsledky shrnuté v tabulce 2. U Spearmanova korelačního koeficientu můžeme pozorovat demonstraci jeho zmíněných vlastností (problém s posuzováním nemonotonních závislostí – Dataset II, a naopak velmi dobrá práce s odlehlými hodnotami – Dataset III). Vzdálenostní korelace se zdá být vhodnou alternativou pro nemonotonní závislosti, ale silně nadhodnocuje „závislost” pro Dataset IV. Vzájemná informace se typově chová nejlépe z uvedených měřítek. U prvních tří datových sad vykazuje vyšší hodnoty (jejich správné uspořádání už je spíše filozofickou otázkou), a u poslední naopak udává hodnotu blízkou nule.
| Dataset I | Dataset II | Dataset III | Dataset IV | |
|---|---|---|---|---|
| Pearson | 0,82 | 0,82 | 0,82 | 0,82 |
| Spearman | 0,82 | 0,69 | 0,99 | 0,50 |
| Vzdálenostní | 0,82 | 0,87 | 0,91 | 0,81 |
| Vzájemná informace | 0,71 | 0,84 | 1,34 | 0,10 |
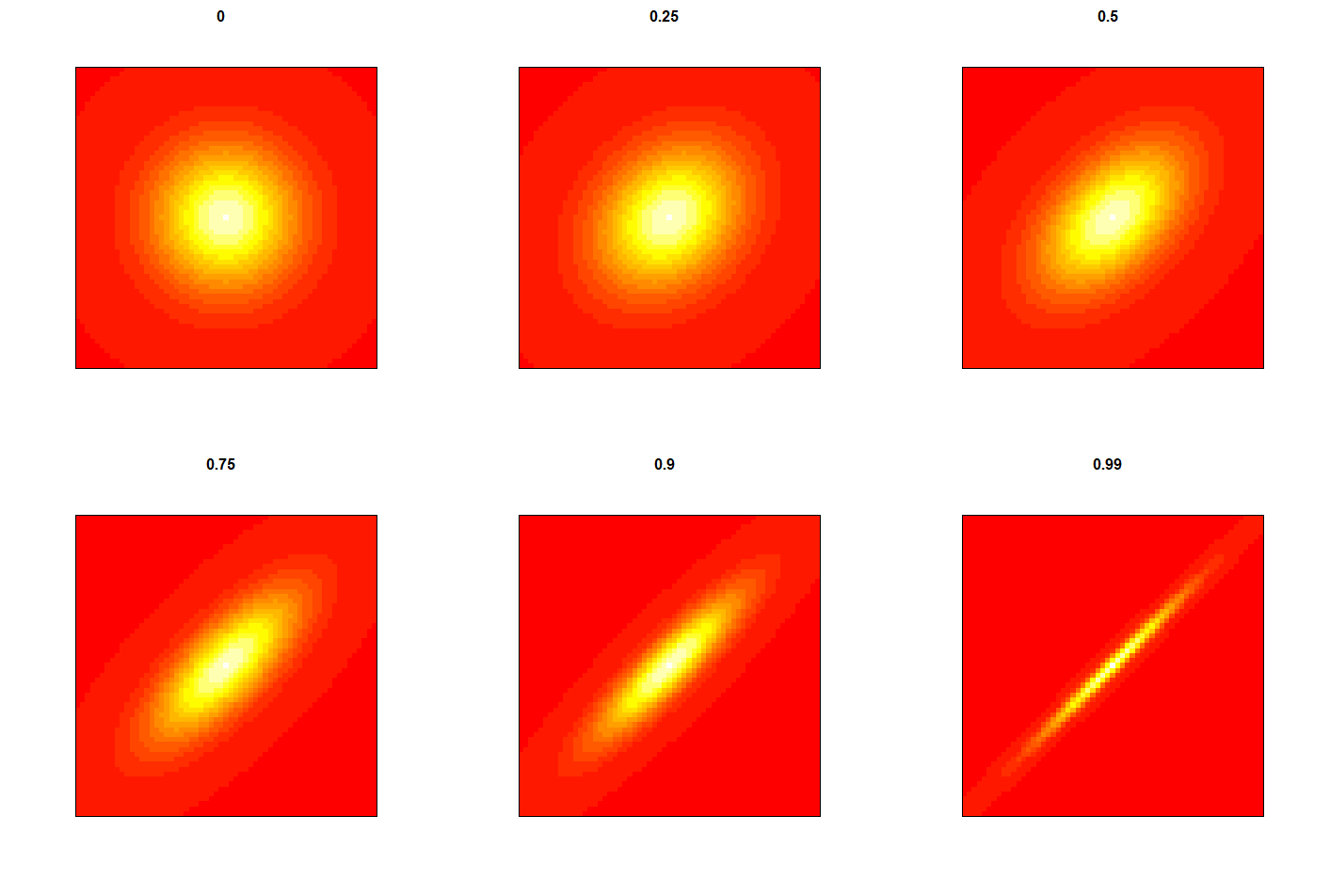
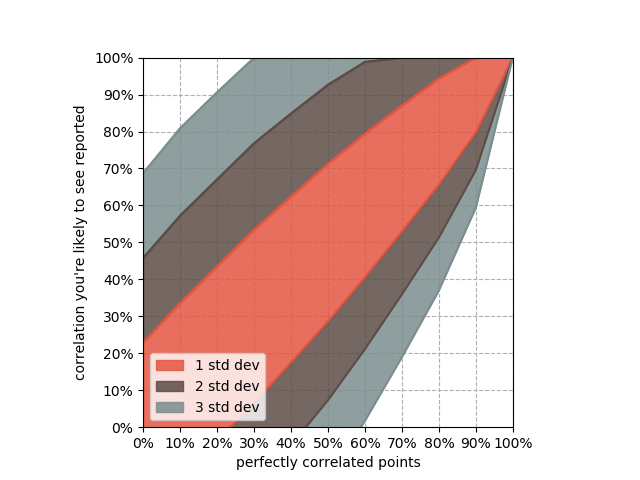
Z níže uvedeného obrázku (obr. 4) je patrný problém společný pro všechny uvedené korelační koeficienty spočívající v nelinearitě jejich informačního přínosu. Na obrázku 4 si lze povšimnout, že např. (Pearsonova) korelace o síle 0,75 má významově blíže k nulové korelaci než k dokonalé. Dokonce i korelace o síle 0,9 má ještě poměrně daleko do dokonalé korelace.
Obrázek 5 pak demonstruje vliv nahodilosti na hodnotu (Pearsonova) korelačního koeficientu na souborech o 20 pozorováních, což obecně není považováno za nedostatečně velký soubor. Je zde patrné, že i při (fakticky) nulové korelaci lze vlivem náhody dosáhnout empirické hodnoty Pearsonovy korelace 0,7. Důsledek tohoto chování lze vystihnout i citací N. N. Taleba na toto téma: „Korelace neimplikuje korelaci”.
Cílem tohoto textu bylo představit čtenáři koncept korelace a ty, kteří jej znají, upozornit na možná úskalí spojená (nejen) s Pearsonovým korelačním koeficientem. Mezi nejdůležitější poselství tohoto textu patří upozornění na existenci vhodných měřítek pro zkoumání (obecné) nezávislosti dat (vzdálenostní korelace, vzájemná informace). Ačkoliv může tento text na čtenáře působit jako snaha o kompromitaci (zejména Pearsonova) korelačního koeficientu, opak je pravdou. Cílem nebylo ukázat, že některý ze zmíněných nástrojů by neměl být používán, ale spíše jako ukázka problémů spojených (zejména, ale ne výlučně) s porušením jejich předpokladů.
Myslíte si, že teď už víte o korelaci vše? Tak se podívejte na https://cs.wikipedia.org/wiki/Simpson%C5%AFv_paradox
[1] F. J. Anscombe. Graphs in statistical analysis. The American Statistician, 27(1):17–21, 1973.
[2] Justin Matejka and George Fitzmaurice. Same stats, different graphs: Generating datasets with varied appearance and identical statistics through simulated annealing. In Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems, CHI ’17, page 1290–1294, New York, NY, USA, 2017. Association for Computing Machinery.
[3] Gábor J. Székely, Maria L. Rizzo, and Nail K. Bakirov. Measuring and testing dependence by correlation of distances. Ann. Statist., 35(6):2769–2794, 12 2007.



Za symbolický zlomový okamžik lze považovat rok 1994, kdy byla v The Advanced Theory of Statistics publikována monografie Bayesian Inference. Hlavní rozdíl obou přístupů je rozdíl mezi klasickou objektivistickou četností a subjektivistickou Bayesovskou interpretací pravděpodobnosti. Připomeňme si stručně základní vlastnosti, vzájemné rozdíly a podívejme se na jejich vyvíjející se vztah podrobněji. Přičemž si vše ukážeme na jednoduchých příkladech.
Klasický přístup, zejména v testování hypotéz, je inspirován rakouským filozofem Karlem Popperem (1902 – 1994) a jeho kritickým racionalismem (pozitivismus, vědecká evoluce, falzifikovatelnost vědeckých teorií). V klasické statistice je pravděpodobnost jevu vnímána jako objektivní vlastnost tohoto jevu, bez ohledu na to, zda ji umíme nebo neumíme určit. Klasická statistika se při odhadech parametrů a testech hypotéz neopírá o pravděpodobnosti vycházející z daného konkrétního výběru, ale o hůře představitelnou situaci všech možných výběrů z dané populace. Problémem pak může být např. určení dostatečně velkého počtu pokusů, splnění nezávislosti pokusů, neměnnost podmínek, apriorní vyloučení jedinečných pokusů či neopakovatelných jevů.
Bayesovská definice pravděpodobnosti je naopak subjektivní a představuje stupeň přesvědčení jednotlivce, že daný jev nastane. Bayesovská statistika tak umožňuje kompletnější záznam o všech zdrojích nejistoty, na kterých je analýza postavena. V Bayesovském přístupu je na začátku každé teorii přiřazena subjektivní pravděpodobnost její platnosti, tzv. apriorní pravděpodobnost, volená na základě všech známých relevantních informací. Při porovnávání dat s teorií se pak zpřesňují výchozí hypotézy právě podle získaných dat a počítá se podmíněná, tzv. posteriorní pravděpodobnost. Bayesovská statistika leží na interpretativních a analytických základech, vztahuje na statistické parametry pravděpodobnostní rozdělení, které kvantifikuje výzkumníkovu nejistotu o hodnotě parametrů.
Subjektivní interpretace pravděpodobnosti má několik výhod. První je její použití vždy tehdy, kdy má daná osoba nějaký názor (přesvědčení, znalost). Další je možnost změny názoru po zisku nových informací. Všechny subjektivní pravděpodobnosti musí být vnitřně konsistentní (koherentní), tedy neodporující základním axiomům ani z nich vyplývajícím pravidlům pro počítání s pravděpodobnostmi. Princip koherence úzce souvisí s racionálním rozhodováním.
Významná námitka proti Bayesovskému přístupu se týkala velké výpočetní náročnosti. To ale padlo s rozvojem a využíváním výpočetní techniky (simulace založené na metodě Monte Carlo a Markovských řetězcích). Parametry pravděpodobnostních rozdělení jsou v klasické statistice označovány za známé či neznámé konstanty, zatímco v Bayesovské jsou to náhodné veličiny, jejichž pravděpodobnostní rozdělení je užitečným nástrojem analýzy.
Zajímavé je, že statistická metodologie byla v 19. století orientovaná převážně Bayesovsky (Bayes, Laplace). V průběhu 20. století byla naopak silně dominantní klasická statistika (Fisher, Pearson), založená na objektivistickém vymezení pravděpodobnosti a statistických úsudků.
Uveďme malou ukázku klasického přístupu k testování hypotéz na velmi zjednodušeném příkladu.
Příklad 1:
Představme si, že někdo přijde s hypotézou, že malé zrzavé holčičky mají nadpřirozené schopnosti. A na nás je rozhodnout, zda tomu tak skutečně je. Nebudeme nyní pro zjednodušení přemýšlet o něčem jako plánování experimentu (Design of Experiments, DoE), najdeme prostě nějaké tři zrzavé holčičky a necháme je každou hodit jedenkrát kostkou. A představme si, že třikrát padne šestka, což může nastat s pravděpodobností 0.0046.
Nulovou hypotézu formulujeme takto: „Zrzavé holčičky nemají nadpřirozené schopnosti“, a v klasické pravděpodobnosti tuto hypotézu na 5% hladině významnosti zamítáme, neboť 0.0046 je menší než 0.05.

□
Naše data něco vypověděla o realitě. Nebezpečí takového přístupu spočívá v tom, že můžeme vymýšlet různé logicky nesmyslné a selským rozumem nepřijatelné hypotézy (což se mimochodem bohužel často děje). V klasické statistice totiž neexistuje nic jako pravděpodobnost hypotézy.
Klasický přístup, který ve statistice výrazně dominoval v minulém století, také mohl mnohdy vést k různým zavádějícím závěrům. Příkladem může být replikační krize ve vědě, která se intenzivně řeší zejména od přelomu tisíciletí (pro zajímavost údaj jednoho výzkumu z roku 2012: z 53 vědeckých studií jich bylo pouze 6 replikovatelných). Synergie špatných pohnutek a nevhodného statistického přístupu (totiž aparát testování hypotéz je automat na generování falešně pozitivních výsledků) tak může mít mimořádně destruktivní vliv.
Řešením může být Bayesovský přístup, který poskytuje formální pravidla pro učení se z dat. Někteří členové Bayesovské komunity tvrdí, že Bayesova věta je nejdůležitější vzoreček na světě :-)
Základní vztahy Bayesovské statistiky jsou:
Řetězové pravidlo $$ \begin{aligned} P (A \cap B) &= P(A | B)P(B) \\ &= P(B | A)P(A) \end{aligned} $$
Úplná pravděpodobnost $$ \begin{aligned} P(A)=\sum\limits_{B} P(A | B)P(B) \end{aligned} $$
Bayesuv vzorec $$ \begin{aligned} P(B | A) &= \frac{P(A \cap B)}{P(A)} \\ &= \frac{ P(A | B)P(B)}{\sum\limits_{B} P(A | B)P(B)} \end{aligned} $$
Ukažme si na jednoduchém příkladu, jak to funguje.
Příklad 2:
Na vybraném místě silnice byla sledována rychlost projíždějících vozidel. Bylo zjištěno, že 30 % projíždějících aut má cizí SPZ a zbytek naši. Z cizích vozidel překročilo rychlost 20 %, z našich 25 %. Určete
a) Pravděpodobnost, že právě projíždějící vozidlo je cizí a překračuje povolenou rychlost.
b) Pravděpodobnost, že právě projíždějící vozidlo překračuje povolenou rychlost.
c) Zjistili jsme, že právě projíždějící auto překračuje rychlost. Jaká je pravděpodobnost, že je cizí?
Zavedeme následující označení:
Značka vozidla \(Z \in \{c=\) cizí\(, n=\) naše\(\}\)
Rychlost vozidla \(R \in \{v =\) vyšší\(, s =\) správná\(\}\)
Pravděpodobnosti hodnot jevu \(Z\) jsou
$$\begin{aligned}P(c) &= 0.3, \\ P(n) &= 0.7 \end{aligned}$$
Podmíněný jev je \(R | Z\) a pravděpodobnosti jeho hodnot jsou
$$ \begin{aligned} P(v | c) &= 0.2, \\ P(v | n) &= 0.25, \\ P(s | c) &= 0.8, \\ P(s | n) &= 0.75 \end{aligned} $$
Řešení a: Ptáme se na sdruženou pravděpodobnost, která je dána řetězovým pravidlem
$$\begin{aligned} P(c \cap v) &= P(v | c)P(c) \\ &= 0.2*0.3 \\ &= 0.6\end{aligned}$$
Řešení b: Hledáme marginální pravděpodobnost pomocí vzorce pro úplnou pravděpodobnost
$$\begin{aligned}P(v) &= P(v | c)P(c)+P(v | n)P(n) \\ &= 0.2*0.3+0.25*0.7 \\ &= 0.235\end{aligned}$$
Řešení c: K určení podmíněné pravděpodobnosti použijeme Bayesův vzorec
$$ \begin{aligned} P(c | v) &= \frac{P(v | c)P(c)}{P(v | c)P(c)+P(v | n)P(n)} \\ &= \frac{0.2*0.3}{0.2*0.3+0.25*0.7} \\ &= 0.255 \end{aligned} $$

□
Nyní ještě jeden ilustrativní příklad, který může být zajímavý zejména vzhledem k nedávné minulosti.
Příklad 3:
Představme si, že existuje nějaká nemoc a testujeme ji nějakým binárním testem (pozitivní či negativní výsledek). Kvalitu testu určují dvě hodnoty – senzitivita (správnost testu na nemocné populaci, tj. podmíněná pravděpodobnost, že test je pozitivní, když jedinec nemoc má) a specificita (správnost testu na zdravé populaci). Nemoc je určena svou prevalencí (jak je v populaci rozšířená, tj. pravděpodobnost, že náhodně vybraný člověk ji má). Zvolme následující hodnoty:
Senzitivita = \(P(T | D)=0.99\)Specificita = \(P(non T | non D) = 0.99\)Prevalence = \(0.001\) (jeden z tisíce je nemocný)
Náhodně vybereme člověka a provedeme jeho testování, přičemž test vyjde pozitivní. Jaká je pravděpodobnost, že tento člověk má testovanou nemoc?
Platí
$$P(D | T)=\frac{P(T | D)P(D)}{[ P(T | D)P(D)+P(T | non D)P(non D)]}$$po dosazení$$ \begin{aligned} P(D | T) &= \frac{Sens*Prev}{[ Sens * Prev + (1-Spec) * (1 - Prev)]} \\ &= \frac{0.99*0.001}{0.99*0.001+0.01*0.999} \\ &= 0.09 \end{aligned} $$
Vychází, že námi náhodně vybraný člověk, jehož test je pozitivní, je nemocný s pravděpodobností 9 %. Uvědomme si, že bez znalosti a užití Bayesovského přístupu by mohlo dojít k výraznému zkreslení reality.
□
Poznamenejme závěrem, že Bayesovský přístup lze uplatnit i v teorii odhadování a řízení. Signály vstupu a výstupu systému jsou zde považovány za náhodné veličiny. Náhodnost v hodnotách měřených dat je možno interpretovat jako vliv určité poruchy, např. jako chyby měření. To je blízké klasickému pojetí.
Navíc ale také neznámé parametry systému je možno považovat za náhodné veličiny. Pak se jedná o čistě Bayesovskou interpretaci náhodnosti, která je způsobena neznalostí příslušných parametrů. Víme, že parametry jsou konstanty, ale jejich přesné hodnoty neznáme a Bayesovsky je popisujeme tak, že specifikujeme všechny jejich možné hodnoty a jejich pravděpodobnosti rozdělení. Tím získávají charakter náhodné veličiny. Ale o tom zas někdy příště.
Zdroje
Albert: Bayesian computation with R, Springer, 2009
Box, Tiao: Bayesian Inference in Statistical Analysis, Addison-Wesley, 1973
Furst: Přednáška Cesta do pekel aneb Jak pervezní incentivy a špatná statistika ničí vědu a výzkum (dostupné na: https://www.youtube.com/watch?v=FAWz2uWim14), 2020
Hebák: Srovnání klasické a Bayesovské pravděpodobnosti a statistiky, Acta Oeconomica Pragensia 1/2012
Hušková: Bayesovské metody, Univerzita Karlova, 1985
Nagy: Základy Bayesovského odhadování a řízení, Vydavatelství ČVUT, 2003