Co je to korelace, k čemu může být užitečná, jaké druhy korelace existují, jak je používat a interpretovat? Odpověď na tyto a některé další otázky nabízí následující text od našeho kolegy Martina Roseckého.
TLDR:
- korelace je obecně měřítko posuzující závislost dvou či více proměnných
- používá-li se Pearsonův korelační koeficient neopatrně, jeho výsledky mohou být velmi zavádějící
- je-li to možné, měly by se závislosti vždy vizualizovat
- korelace o velikosti 0,5 je svým informačním přínosem výrazně blíže nulové korelaci než dokonalé
- pro posuzování nelineárních závislostí je vhodné využít vzdálenostní korelaci či vzájemnou informaci
Co je to korelace a k čemu je dobrá?
V životě člověka je poměrně běžné hledat a posuzovat souvislosti mezi rozličnými jevy, ať už si to uvědomujeme, nebo ne. Příkladem mohou být otázky jako: Nakolik souvisí výsledky ve volebním průzkumu či modelu s reálným výsledkem voleb a jak se tato souvislost mění v čase? Jak moc mi bude špatně, když zkonzumuji větší množství jídla či alkoholu než obvykle? Jakým směrem a jak výrazně se pohne cena kryptoměny na základě tweetu Elona Muska? Jak velký přínos bude mít, když se budu večer před písemkou učit místo toho, abych navštívil oblíbené restaurační zařízení? Lze z níže uvedené fotografie usoudit, že kočky způsobují pády střech?
#Correlation is not #Causation pic.twitter.com/3csdhaGmee
— john gonder infosec.exchange/@packetlevel (@packetlevel) October 22, 2021
Výše zmíněné otázky více či méně míří na koncept korelace. Korelace by se v obecném smyslu dala popsat jako měřítko, které dokáže vystihnout toto chování: když hodnota jedné proměnná roste, roste (pozitivní korelace), příp. klesá (negativní korelace) i druhá. Laicky řečeno je korelace hodnota, která říká, jak moc spolu sledované proměnné souvisí.
Příkladem může být třeba množství prodané zmrzliny a teplota vzduchu. Dá se očekávat, že v teplejších dnech bude množství prodané zmrzliny vyšší oproti chladnějším dnům.
Velmi důležitým pojmem při použití korelace je i kauzalita neboli příčinnost. Ta zjednodušeně řečeno říká, zda je jeden jev příčinnou druhého (v uvedeném příkladu vyšší teplota způsobuje vyšší prodej zmrzlin). Narozdíl od korelace však kauzalita není symetrická (z výše uvedeného je zřejmé, že ani symetrická být nemůže). Navíc “přítomnost” korelace neznamená, že nutně mezi oběma proměnnými existuje i kauzální vztah (odtud ono známé – korelace neimplikuje kauzalitu). Co to znamená prakticky? Když k uvedenému příkladu přidáme ještě údaje o počtu požárů, mohlo by někoho na základě korelace napadnout, že v rámci prevence požárů bude dobré zakázat prodej zmrzliny, což zřejmě nebude příliš funkční opatření.
Pearsonův korelační koeficient a jeho nedostatky
Pojem korelace se v médiích objevuje zejména v souvislosti s děním na trzích, se studiemi týkajícími se vlivu nějakého faktoru na zdraví člověka či se sociologickými/ psychologickými studiemi. Tento pojem standardně bývá i součástí základních kurzů statistiky a pravděpodobnosti, přičemž se v drtivé většině jedná o tzv. Pearsonův korelační koeficient. Jeho praktické využití má však více úskalí než se může na první pohled zdát (zvlášť pro člověka bez hlubších znalostí a zkušeností).
Pearsonův korelační koeficient závisí zejména na hodnotě kovariance. Její hodnota roste v případě, že jsou hodnoty sledovaných proměnných obě vyšší než průměr, resp. nižší než průměr, v opačném případě hodnota kovariance klesá. Toto chování ukazuje na důležitost 2 základních předpokladů: linearita závislosti mezi proměnnými a normalita sdruženého rozdělení zkoumaných proměnných. Hodnoty směrodatné odchylky, příp. rozptylu, zajišťují pouze škálování kovariance na interval [-1,1]. V případě porušení uvedených předpokladů může být chování Pearsonova korelačního koeficientu značně neočekávané (viz obr. 1, pro který vychází hodnota korelačního koeficientu rovna 0,66, přičemž je zde patrná dokonalá exponenciální závislost).

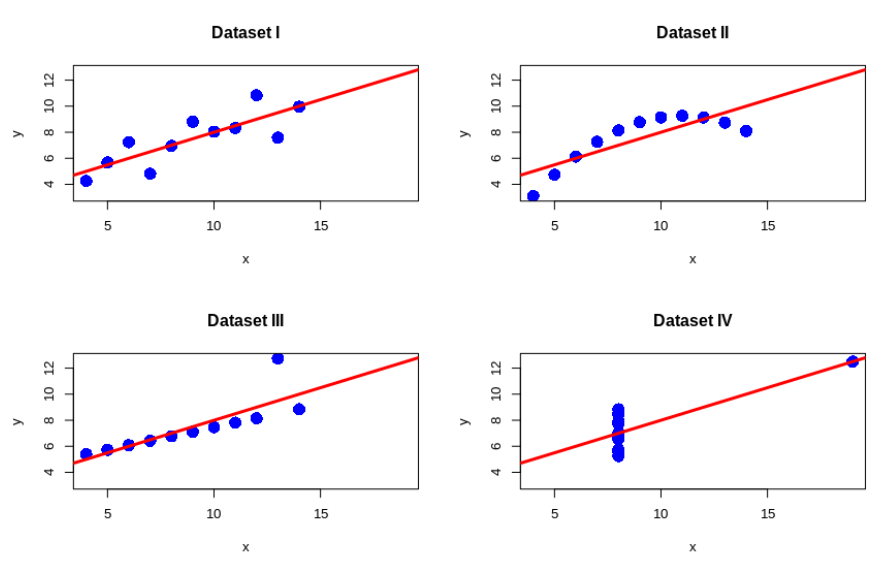
Zmíněné problémy nejsou ničím novým pod sluncem. Poměrně známý je příklad Anscombe (1973, [1]), který uvádí čtveřici statistických souborů (viz obr. 2). Tyto soubory mají stejné nebo alespoň velmi podobné hodnoty základních sumarizačních charakteristik (výběrové průměry, rozptyly, korelaci), a také (lineární) regresní model (včetně koeficientu determinace), viz tab. 1. Tento příklad, podobně jako projekt Datasaurus ([2], viz obr. 3), primárně nekritizuje používání (Pearsonova) korelačního koeficientu. Snaží se spíše upozornit na nutnost vizualizace dat oproti jejich prostému shrnutí prostřednictvím základních měřítek (viz obě zmíněné datové sady).
| Charakteristika | Hodnota | Přesnost |
|---|---|---|
| Průměr x | 9 | přesné |
| Rozptyl x | 11 | přesné |
| Průměr y | 7,5 | 2 desetinná místa |
| Rozptyl y | 4,125 | ± 0,003 |
| Korelace | 0,816 | 3 desetinná místa |
| Lineární regresní model | y = 3,00 + 0,50x | 2 resp. 3 desetinná místa |
| R2 | 0,67 | 2 desetinná místa |

V roce 2019 se Pearsonův korelační koeficient ocitl pod silnou kritikou N. N. Taleba. Přesněji řečeno šlo spíše o kritiku jeho nesprávného používání (při nesplnění předpokladů), zejména v sociálních vědách.
Zde byly prezentovány a demonstrovány mj. následující problémy:
- nesprávná interpretace informační hodnoty poskytované korelačním koeficientem
- nesprávné použití korelace pro nelineární závislosti.
Obecným problémem s korelacemi (zejména při menším množství dat) jsou tzv. spurious correlations. Ty odkazují na situace, kdy jsou sice nějaké proměnné silně korelovány, ale neexistuje mezi nimi žádný kauzální vztah (např. počet absolventů PhD studia a množství uranu uloženého v amerických jaderných elektrárnách). Takové situace mohou vzniknout pouze dílem náhody (při dostatečném množství náhodně generovaných proměnných se dříve nebo později objeví silná korelace). Dalším případem falešných korelací je situace, kdy jsou 2 proměnné (např. počet požárů a množství prodané zmrzliny) „svázány” prostřednictvím třetí proměnné (zde např. průměrná denní teplota), která buď není nebo nemůže být pozorována.
Alternativy
V této části budou stručně popsána další vybraná měřítka pro měření závislosti v datech. Spearmanův korelační koeficient se používá jako nejčastější alternativa k Pearsonovu, zejména pokud dojde k porušení jeho předpokladů. Vzdálenostní korelace je novým a nepříliš známým přístupem k tomuto problému. Vzájemná informace je pak navrhována N. N. Talebem.
- Spearmanův korelační koeficient vznikne použitím pořadí hodnot místo skutečných hodnot (jedná se tedy o tzv. neparametrický přístup). V důsledku použití pořadí namísto skutečných hodnot je Spearmanův korelační koeficient velmi robustní. Největším (a prakticky jediným zásadním) omezením tohoto přístupu je požadavek na monotonii zkoumané závislosti.
- Vzdálenostní korelace (Distance correlation) zobecňuje Pearsonův korelační koeficient ve dvou ohledech: 1. lze ji spočítat pro dvojici vektorů různých dimenzí a 2. nulová vzdálenostní korelace značí nezávislost zkoumaných vektorů. Narozdíl od Pearsonova a Spearmanova korelačního koeficientu se hodnota vzdálenostní korelace pohybuje v intervalu [0,1]. Empirické výsledky [3] naznačují, že vzdálenostní korelace je citlivá na všechny případy nelineárních či nemonotonních závislostí.
- Vzájemná informace (Mutual information). Vzájemnou informaci lze zjednodušeně chápat jako “vzdálenost” mezi sdruženým rozdělením zkoumaných proměnných a součinem jejich marginálních rozdělení. Laicky se “měří” jak dobře lze rekonstruovat informace, které jsou k dispozici pokud je známa souvislost mezi nimi oproti situaci, kdy ji neznáme. Formálně se pro měření používá tzv. relativní entropie (známá jako Kullback-Leiblerova divergence, používána v mnoha dalších odvětvích). Vzájemná informace je nezáporná, přičemž nulová je pouze pokud jsou zkoumané veličiny nezávislé. Z hlediska praktické využitelnosti je u vzájemné informace nepříjemné, že narozdíl od korelačních koeficientů není škálovaná. Její využití pro kvantifikaci síly závislosti je tedy problematičtější než u uvedených korelačních koeficientů.
Demonstrace
Nejprve se vraťme k problému nutnosti vizualizace dat, konkrétně k Anscombově kvartetu (viz obr. 2). Výše byla zmíněna neschopnost Pearsonova korelačního koeficientu rozlišit typově výrazně odlišné závislosti. Nabízí se tedy jednoduchá otázka: dokáže některé ze zkoumaných měřítek odhalit, že se jedná o výrazně odlišné závislosti? Jako vodítko nám poslouží výsledky shrnuté v tabulce 2. U Spearmanova korelačního koeficientu můžeme pozorovat demonstraci jeho zmíněných vlastností (problém s posuzováním nemonotonních závislostí – Dataset II, a naopak velmi dobrá práce s odlehlými hodnotami – Dataset III). Vzdálenostní korelace se zdá být vhodnou alternativou pro nemonotonní závislosti, ale silně nadhodnocuje „závislost” pro Dataset IV. Vzájemná informace se typově chová nejlépe z uvedených měřítek. U prvních tří datových sad vykazuje vyšší hodnoty (jejich správné uspořádání už je spíše filozofickou otázkou), a u poslední naopak udává hodnotu blízkou nule.
| Dataset I | Dataset II | Dataset III | Dataset IV | |
|---|---|---|---|---|
| Pearson | 0,82 | 0,82 | 0,82 | 0,82 |
| Spearman | 0,82 | 0,69 | 0,99 | 0,50 |
| Vzdálenostní | 0,82 | 0,87 | 0,91 | 0,81 |
| Vzájemná informace | 0,71 | 0,84 | 1,34 | 0,10 |
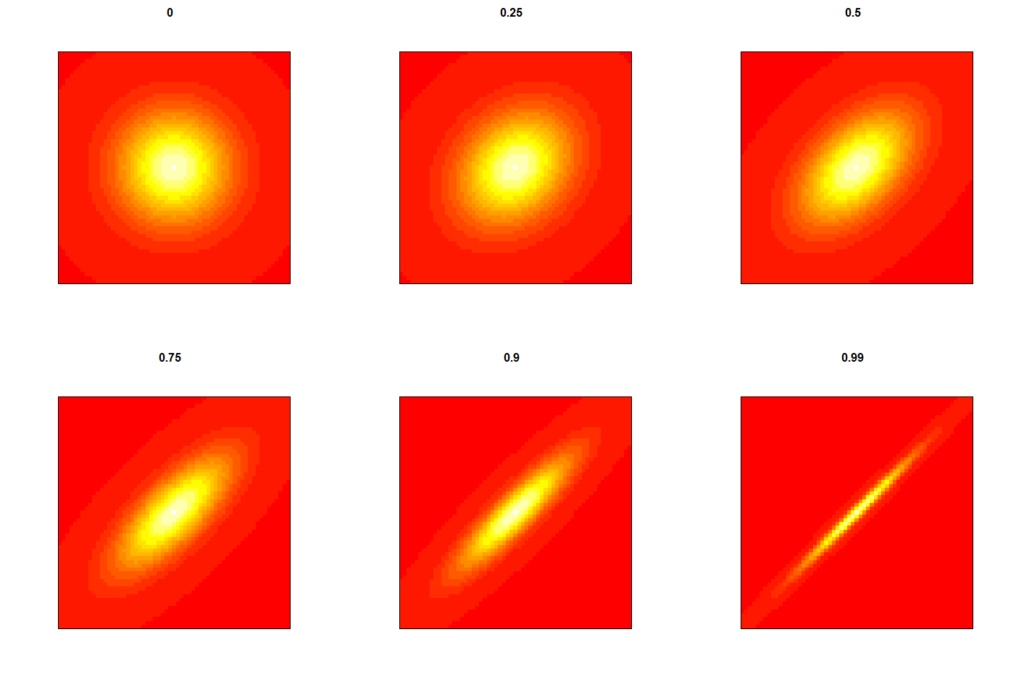
Z níže uvedeného obrázku (obr. 4) je patrný problém společný pro všechny uvedené korelační koeficienty spočívající v nelinearitě jejich informačního přínosu. Na obrázku 4 si lze povšimnout, že např. (Pearsonova) korelace o síle 0,75 má významově blíže k nulové korelaci než k dokonalé. Dokonce i korelace o síle 0,9 má ještě poměrně daleko do dokonalé korelace.
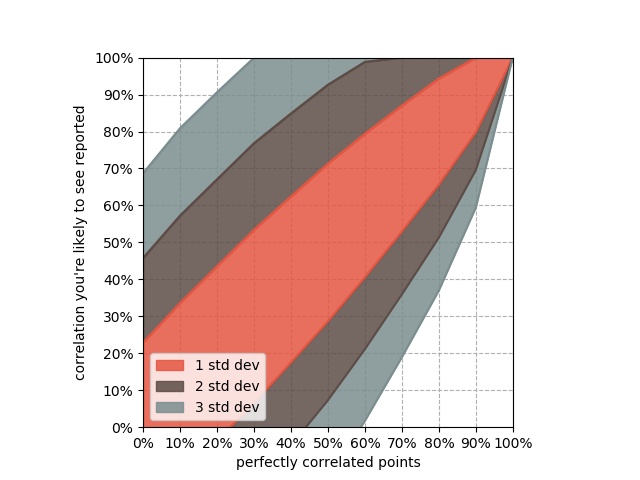
Obrázek 5 pak demonstruje vliv nahodilosti na hodnotu (Pearsonova) korelačního koeficientu na souborech o 20 pozorováních, což obecně není považováno za nedostatečně velký soubor. Je zde patrné, že i při (fakticky) nulové korelaci lze vlivem náhody dosáhnout empirické hodnoty Pearsonovy korelace 0,7. Důsledek tohoto chování lze vystihnout i citací N. N. Taleba na toto téma: „Korelace neimplikuje korelaci”.
Shrnutí
Cílem tohoto textu bylo představit čtenáři koncept korelace a ty, kteří jej znají, upozornit na možná úskalí spojená (nejen) s Pearsonovým korelačním koeficientem. Mezi nejdůležitější poselství tohoto textu patří upozornění na existenci vhodných měřítek pro zkoumání (obecné) nezávislosti dat (vzdálenostní korelace, vzájemná informace). Ačkoliv může tento text na čtenáře působit jako snaha o kompromitaci (zejména Pearsonova) korelačního koeficientu, opak je pravdou. Cílem nebylo ukázat, že některý ze zmíněných nástrojů by neměl být používán, ale spíše jako ukázka problémů spojených (zejména, ale ne výlučně) s porušením jejich předpokladů.
Myslíte si, že teď už víte o korelaci vše? Tak se podívejte na https://cs.wikipedia.org/wiki/Simpson%C5%AFv_paradox
Reference
[1] F. J. Anscombe. Graphs in statistical analysis. The American Statistician, 27(1):17–21, 1973.
[2] Justin Matejka and George Fitzmaurice. Same stats, different graphs: Generating datasets with varied appearance and identical statistics through simulated annealing. In Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems, CHI ’17, page 1290–1294, New York, NY, USA, 2017. Association for Computing Machinery.
[3] Gábor J. Székely, Maria L. Rizzo, and Nail K. Bakirov. Measuring and testing dependence by correlation of distances. Ann. Statist., 35(6):2769–2794, 12 2007.
